# 빅데이터분석기사 실기 이기적 학습 내용
데이터 전처리
- 문자로 된 범주형 데이터는 처리하기 편하게 숫자로 표현을 바꿈
- 월요일은 1, 화요일은 2로 인코딩 시키거나, 수치 데이터의 분포를 정규화함
표준정규화
- 데이터의 범위가 같아지도록 변수별로 값을 비례적으로 조정하는 과정(데이터 스케일링)
- 대표적인 기법으로 표준정규화, Min-Max 정규화가 있다.
한국인 천명의 연간 육류 소비량이 53.9kg, 표준편차 5kg의 정규분포를 따르고, 일본 성인 남성 천명의 육류 소비량은 32.7kg, 표준편차 4kg의 정규분포를 따른다고 하였을때 두 집단의 육류소비량 평균이 0, 표준편차가 1인 표준정규분포로 표준화를 해본다
import pandas as pd
import numpy as np
#1000명의 데이터를 난수로 만듦
korea =5*np.random.randn(1000)+53.9
japan =3*np.random.randn(1000)+32.7
consumption = pd.DataFrame({'한국인':korea, '일본인':japan}) # 딕셔너리로 삽입
consumption.
① Z-표준화
- Z-score는 각 데이터 값에서 평균을 뺀 후 표준편차로 나누어 준 값이다.
방법1) numpy >> (x-mean(x))/std(x)
방법2) scipy.stats >> zscore()
방법3) sklearn.preprocessing >> StandardScaler().fit_transform()
import scipy.stats as ss
consumption["한국인정규화"] = ss.zscore(korea)
consumption["일본인정규화"] = ss.zscore(japan)
consumption.head(5)
②Min-Max 정규화
- Min-Max 정규화는 연속형 변수의 값을 0과 1사이의 값으로 변환한다.
스케일이 다른 두 변수를 min-max 변환하면 상호간에 비교가 가능하다
- 사이킷런 패키지의 MinMaxScaler(), minmax_scale() 함수를 이용하는 방법이나, 넘파이 패키지의 통계함수를 이용해 직접 입력하는 방식이 있다.
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler()
consumption["한국인민맥스"] = sc.fit_transform(consumption[["한국인"]])
consumption["일본인민맥스"] = sc.fit_transform(consumption[["일본인"]])
# 이유는 모르겠으나 [] 괄호를 두번해줘야 실행이 됨
consumption.head(5)
③ 왜도 계산 (skew)
- 왜도(분포의 대칭 척도)는 scipy의 skew()함수 사용
#변호사들이 평가한 고등법원판사 데이터
df = pd.read_csv("https://raw.githubusercontent.com/YoungjinBD/dataset/main/USJudgeRatings.csv")
df.head(5)
#왜도를 구하는 것은 간단함
import scipy.stats as ss
print(ss.skew(df["CONT"]))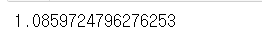
④ 차원축소 : PCA(주성분 분석)
- 주성분 분석은 상관성이 높은 여러 변수들의 선형조합으로 만든 새로운 변수들로 요약, 축소하는 기법
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#데이터 준비하기 (꽃에 대한 data)
iris = pd.read_csv("https://raw.githubusercontent.com/YoungjinBD/dataset/main/iris.csv")
PCA에서는 '연속형 변수'만 사용하기 떄문에 '범주형 변수'(문자인 species)를 분리한다.

변수간의 스케일 차이가 나면 주성분에 영향을 주기 떄문에 변수를 표준화나 정규화를 시켜준다.
from sklearn.preprocessing import StandardScaler
#sklearn을 활용한 정규화
df1["sepal_length"] = StandardScaler().fit_transform(df1[["sepal_length"]])
df1["sepal_width"] = StandardScaler().fit_transform(df1[["sepal_width"]])
df1["petal_length"] = StandardScaler().fit_transform(df1[["petal_length"]])
df1["petal_width"] = StandardScaler().fit_transform(df1[["petal_width"]])
#PCA 수행
from sklearn.decomposition import PCA
#변환할 차원의 수
pca = PCA(n_components=4)
p_score=pca.fit_transform(df1)
print(p_score.shape)
print(pca.explained_variance_ratio_)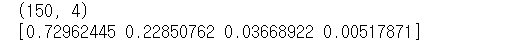
explained_variance_ratio_는 각각 차원의 기여도를 나타낸다.
첫번째 차원 만으로 전체 변동성의 72.9%를 설명할 수 있고, 두번째 차원은 22.8%를 차지하므로
2개 요소(차원)으로만 변환해도 원본데이터의 변동성을 95.8% 설명 가능하므로,
변수를 원래 4개에서 2개로 줄일 수 있다.
⑤결측치 처리
1) 결측치의 식별
- info() 함수를 사용해 개수를 확인함
- isnull() 함수를 사용해 찾을 수 있음 (결측치인 경우 True 반환)
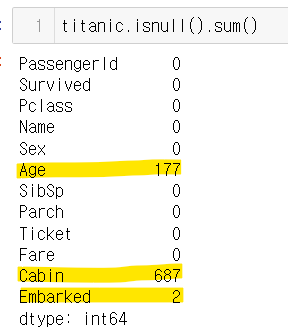
2) 결측치의 대체
- 단순대치법, 다중대치법이 있음
a. 결측치가 있는 행 전체를 데이터셋에서 제거
=> dropna() 함수를 사용해 결측치가 있는 행 전체를 제거

b.결측치를 지정값으로 대체
=> fillna() 함수를 사용해 지정값으로 대체
# 결측치가 있던 age의 값을 평균값으로 대체해보자
df=titanic
age_mean= df["Age"].mean()
df["Age"].fillna(age_mean,inplace=True)
df["Age"].isnull().sum()
c.결측치를 인접한 값으로 대체
=> fillna(), 함수에 method="ffill옵션을 추가하면 됨 "
df["Age"].fillna(method="ffill",inplace=True)
df["Age"].isnull().sum()
⑥ 이상치 처리
- 이상값은 데이터 범위에서 크게 벗어난 값이다.
- 사분위범위, 정규분포를 이용해 식별하고, 제거 여부를 판단한다.
이상치가 있는 랜덤데이터 만들기
import numpy as np
import pandas as pd
data = 10*np.random.randn(200) + 50
df= pd.DataFrame({"값":data})
# 강제로 이상값을 넣는다.
df.loc[201] =2
df.loc[202] = 100
df.loc[203] = 10
df.loc[204]= 110
IQR(사분위범위) 방법
# boxplot이 일반적이지만 시험에는 그래프를 못보는걸로 알고있어 넘어간다
- 사분위 범위는 quantile() 함수나 describe() 함수를 이용해 구한다.
Q1 =df["값"].quantile(.25) # 하위 25% - 1분위
Q2 =df["값"].quantile(.50) # 50% - 2분위
Q3 =df["값"].quantile(.50) # 75% (상위 25%) - 3분위
IQR= Q3-Q1
IQR
이상치는 (3분위+IQR*1.5) 보다 큰 값 이거나, (1분위-IQR*1.5) 보다 작은 값으로 검출 할 수 있다.
=> boxplot을 상상하면 쉽다.
upperC=df[df["값"]>(Q3+IQR*1.5)]
lowerC=df[df["값"]<(Q1-IQR*1.5)]
print(upperC)
print(lowerC)
'IT&게임 > 빅데이터분석기사(빅분기)' 카테고리의 다른 글
| 빅데이터분석기사 제2유형 : ① EDA (0) | 2024.06.04 |
|---|---|
| 빅데이터 분석기사 - 1유형 예제문제 학습하기(결측치2) (0) | 2024.06.03 |
| 빅데이터 분석기사 - 1유형 예제문제 학습하기(결측치) (3) | 2024.06.02 |
| 빅데이터분석기사 실기 공부하기- 제1유형 : 데이터 전처리① (1) | 2024.05.30 |
| 빅데이터분석기사 비전공자/직장인 공부 방법 및 후기 (2) | 2024.04.21 |


댓글